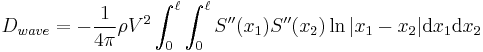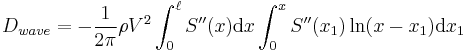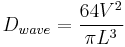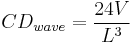Sears–Haack body
The Sears–Haack body is the aerodynamic body shape with the lowest theoretical wave drag. Aircraft designed to operate at high subsonic or supersonic speeds have their cross-sectional areas designed to match as closely as possible the proportions of Sears-Haack body.
By Whitcomb's area rule, the derivative of cross-sectional area gives wave drag. Thus, the Sears–Haack body is pointed at two ends and grows to a maximum and then decreases toward the second point.
Under the area rule, shapes with the same cross-sectional area at each point along their length as this shape have the minimal amount of wave drag, and the overall shape of many aircraft designed with transonic flight considerations have cross-sectional areas that approach this form (despite appearances).
The derivation and shape were published independently by two separate researchers: Wolfgang Haack in 1941 and later by William Sears in 1947.[1]
Contents |
Useful Formulas
The cross sectional area of a Sears–Haack Body is:
The volume of a Sears–Haack Body is:
The radius of a Sears-Haack Body is:
The derivative (slope) is:
The 2nd derivative is:
where:
x is the ratio of the distance from the nose to the whole body length. This is always between 0 and 1.
r is the radius
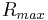 is the radius at its maximum (occurs at center of the shape)
is the radius at its maximum (occurs at center of the shape)
V is the volume
L is the length
 is the density
is the density
U is the velocity
From Slender-body theory:
alternatively:
These formulas may be combined to get the following:
See also
References
- ^ Palaniappan, Karthik (2004). "Bodies having Minimum Pressure Drag in Supersonic Flow - Investigating Nonlinear Effects". 22nd Applied Aerodynamics Conference and Exhibit, Antony Jameson. http://aero-comlab.stanford.edu/Papers/palaniappan.aiaa.04-5383.pdf. Retrieved 2010-09-16.
![A(x) = \frac {16V}{3L\pi}[4x-4x^2]^{3/2} = \pi R_{max}^2[4x-4x^2]^{3/2}](/2012-wikipedia_en_all_nopic_01_2012/I/d0674568afb6c78117465455ef205bce.png)
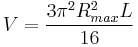
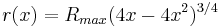
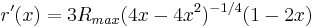
![r''(x) = -3R_{max}[({4x-4x^2})^{-5/4} {(1-2x)^2} %2B 2(({4x-4x^2})^{-1/4})]](/2012-wikipedia_en_all_nopic_01_2012/I/12524a2c43c86ce5acb060e6c711cae6.png)